The particle swarm algorithm was first presented by (Eberhard and Kennedy, 1995). It is inspired by the social behaviour in a flock of individuals. It is generally slower than the complex algorithm, but may offer a higher chance for convergence. The method works as follows:

Generate a population of random particle in the parameter space.
Initialize the best known point for each particle to its own position: $p_{i}=x_{i}$
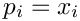
Initialize the velocity of the particle to a random value
Simulate each particle and evaluate objective functions
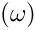
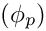
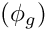
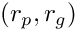
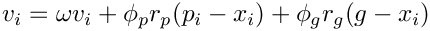
Update each particle's velocity, by using a weight factor $(\omega)$ , two "gravities", one towards the particle's own best point $(\phi_{p})$ and one towards the global best known points $(\phi_{g})$ , with randomization factors $(r_{p},r_{g})$ : $v_{i} = \omega v_{i}+\phi_{p}r_{p}(p_{i}-x_{i})+\phi_{g}r_{g}(g-x_{i})$

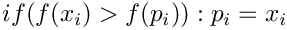
Update each particle's best known point if the new position is better: $if(f(x_{i})>f(p_{i})): p_{i}=x_{i}$

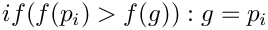
Update the swarms best known point if one of the new points is better: $if(f(p_{i})>f(g)): g=p_{i}$
Repeat from point 4 until convergence

References

Eberhart, R. C. and Kennedy, J. A new optimizer using particle swarm theory. Proceedings of the Sixth International Symposium on Micromachine and Human Science, Nagoya, Japan. pp. 39-43, 1995.