The constrained simplex algorithm, also known as the complex algorithm, is based upon the simplex method developed by (Spendley et al, 1962) and (Nelder & Mead, 1965). It was first presented by (Box, 1965) and later improved by (Guin, 1968).

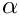
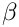
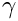
To optimize a model with n tunable parameters, we use k≥n+1 points in an n-dimensional parameter space, typically k=2n. The most important settings are the reflection coefficient $\alpha$ , the randomization factor $\beta$ and the forgetting factor $\gamma$ . The following procedure is used:

Assign random values to each point.
Simulate and evaluate the objective function for each point.
Reflect the worst point $(x_{w})$ through the geometric centre $(x_{c})$ of the other points, using the following formula:

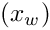
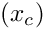
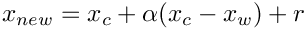
$x_{new}=x_{c}+\alpha(x_{c}-x_{w})+r$
Check for convergence in function values
Check for convergence in parameter values

Reduce objective value of the non-mirrored point with the forgetting factor
Restart at point 2

References

Spendley W., Hext G. R., and Himsworth F. R., “Sequential application of Simplex designs in optimisation and evolutionary operation,” Technometrics, vol. 4, pp. 441-462, 1962.

Nelder J. A. and Mead R., “A simplex method for function minimization,” Computer Journal, vol. 7, pp. 308-313, 1965.

Box M. J., “A new method of constraint optimization and a comparison with other methods,” Computer Journal, vol. 8, pp. 42-52, 1965.

Guin J. A., “Modification of the Complex method of constraint optimization,” Computer Journal, vol. 10, pp. 416-417, 1968.